Geometric Representations: SDFs & Voxelization

Problem / Goal

This project investigates the fundamental differences between explicit representations (triangle meshes) and implicit representations (Signed Distance Functions) in computational geometry.

The core objective was to implement robust algorithms for converting between these forms, specifically focusing on voxelization via ray-casting and surface reconstruction via Marching Cubes.

My Contribution

I implemented a custom geometry processing pipeline from scratch in Python. My key contributions included:

• Robust Voxelization: A ray-casting algorithm to convert explicit Triangle Meshes (.STL) into binary Voxel Grids.
• SDF Primitives & Boolean Ops: A library of vectorized distance functions (Sphere, Box, Torus) and CSG operations.
• Marching Cubes Reconstruction: Bridging the gap back to explicit geometry by extracting isosurfaces from volumetric data.
• Spatial Optimization: Optimizing intersection tests using bounding box pruning.

Technical Approach

1. Robust Voxelization (Ray-Casting)

I implemented a custom voxelizer that robustly handles geometry by shooting rays through a grid. The process shoots rays through the grid and counts intersections with the mesh. By the Jordan Curve Theorem, an odd number of intersections implies a point is inside the mesh.

# Cast a ray at each grid point
ray_direction = np.array([0.0, 0.0, 1.0])
for i in range(0, nx):
    for j in range(0, ny):
        # shoot a ray from the center of this voxel column
        ray_origin = voxel_grid_min + dx * np.array([i + 0.5, j + 0.5, 0.0])
        
        # triangles from step 2.2 that might intersect this ray
        triangles_to_check = tris_to_test[i][j]
        intersections = []
        for tri in triangles_to_check:
            t = triangle_ray_intersection(tri, ray_origin, ray_direction)
            if t > 0:  # only count intersections in front of the ray
                intersections.append(t)
        
        intersections.sort()
        # go through each voxel in z and check if we're inside the mesh
        for k in range(nz):
            voxel_z_center = voxel_grid_min[2] + (k + 0.5) * dx
            t_center = voxel_z_center - ray_origin[2]

            # count how many intersections are before this voxel
            # if odd -> inside, even -> outside
            num_hits = sum(1 for t in intersections if t < t_center)
            if num_hits % 2 == 1:
                voxels[i, j, k] = 1

2. SDF Primitives & Boolean Ops

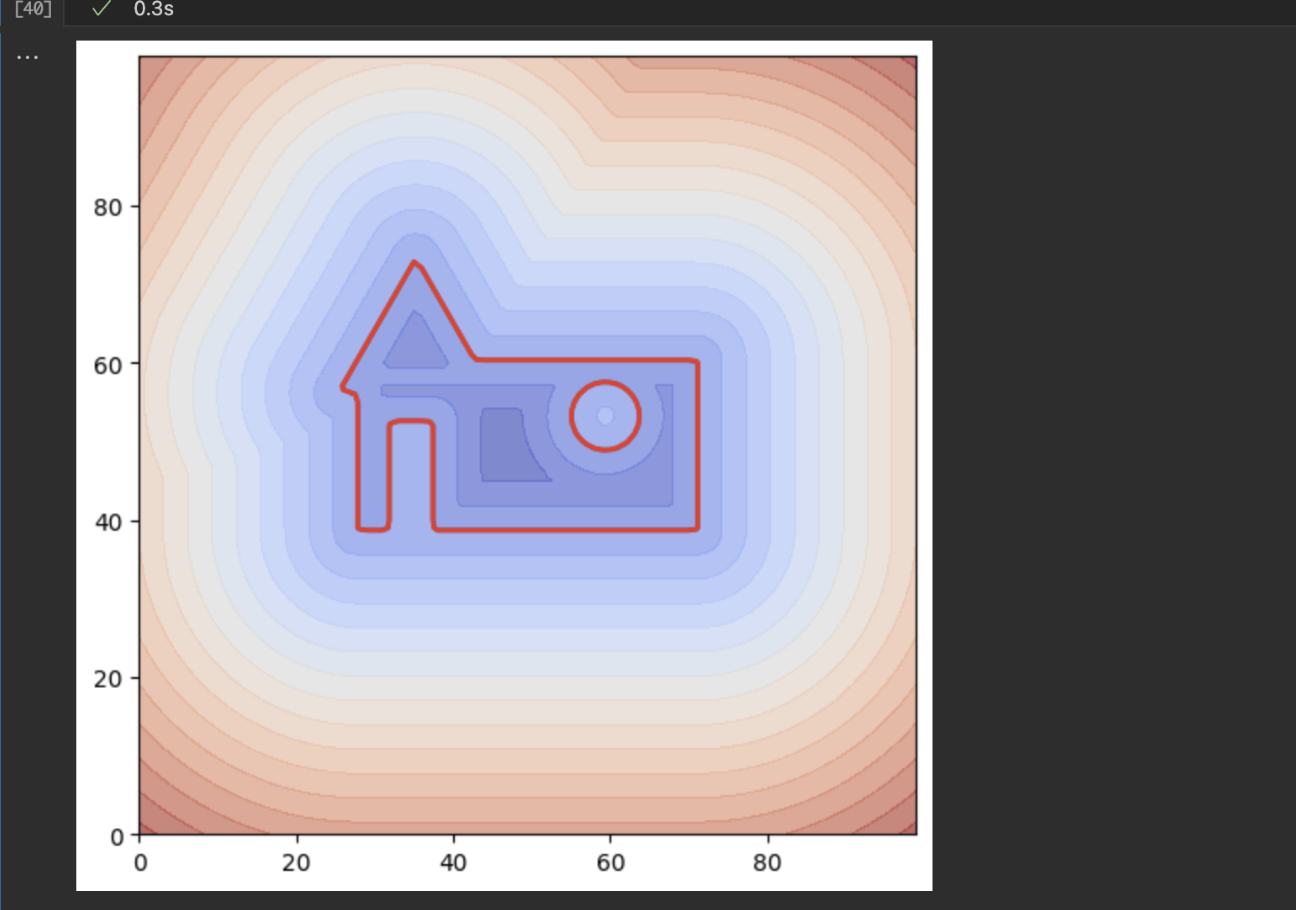
Complex shapes are composed by combining simple primitives. I built an SDF library where shapes are defined by mathematical functions, and composition is achieved via boolean operations (min/max).

def op_union(sdf1, sdf2):
    """ Union of two SDFs (minimum distance) """
    return np.minimum(sdf1, sdf2)

def op_intersection(sdf1, sdf2):
    """ Intersection of two SDFs (maximum distance) """
    return np.maximum(sdf1, sdf2)

def op_difference(sdf1, sdf2):
    """ Difference of two SDFs (max of sdf1 and -sdf2) """
    return np.maximum(sdf1, -sdf2)

Validation / Results

The pipeline was validated by converting complex meshes to voxels and regenerating surfaces from SDFs. The results demonstrate accurate geometric processing with minimal artifacts.

Lessons + Next Steps

Lesson: Implementing geometric algorithms from scratch highlights the importance of numerical stability, especially when dealing with ray-triangle intersections and floating-point errors.

Next Steps: Extending the system to support Constructive Solid Geometry (CSG) tree parsing directly from a script files or integrating with a real-time renderer.

Links