AI-Driven Material Discovery
Bayesian Optimization, Multi-Objective Design
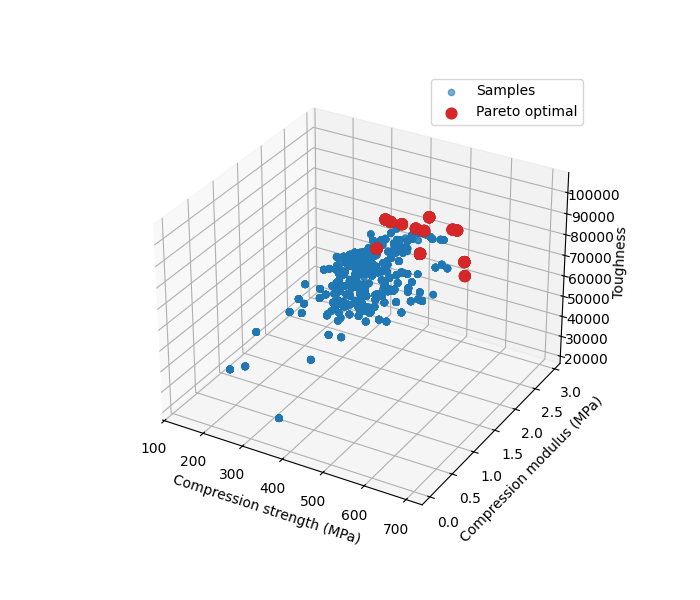
- What I built: A Bayesian Optimization framework to discover high-performance photopolymer mixtures.
- Why it matters: Testing every chemical combination is impossible; AI guides the search to optimal regions efficiently.
- Proof: Achieved a 288× improvement in the sampled performance space compared to random search.
Problem / Goal
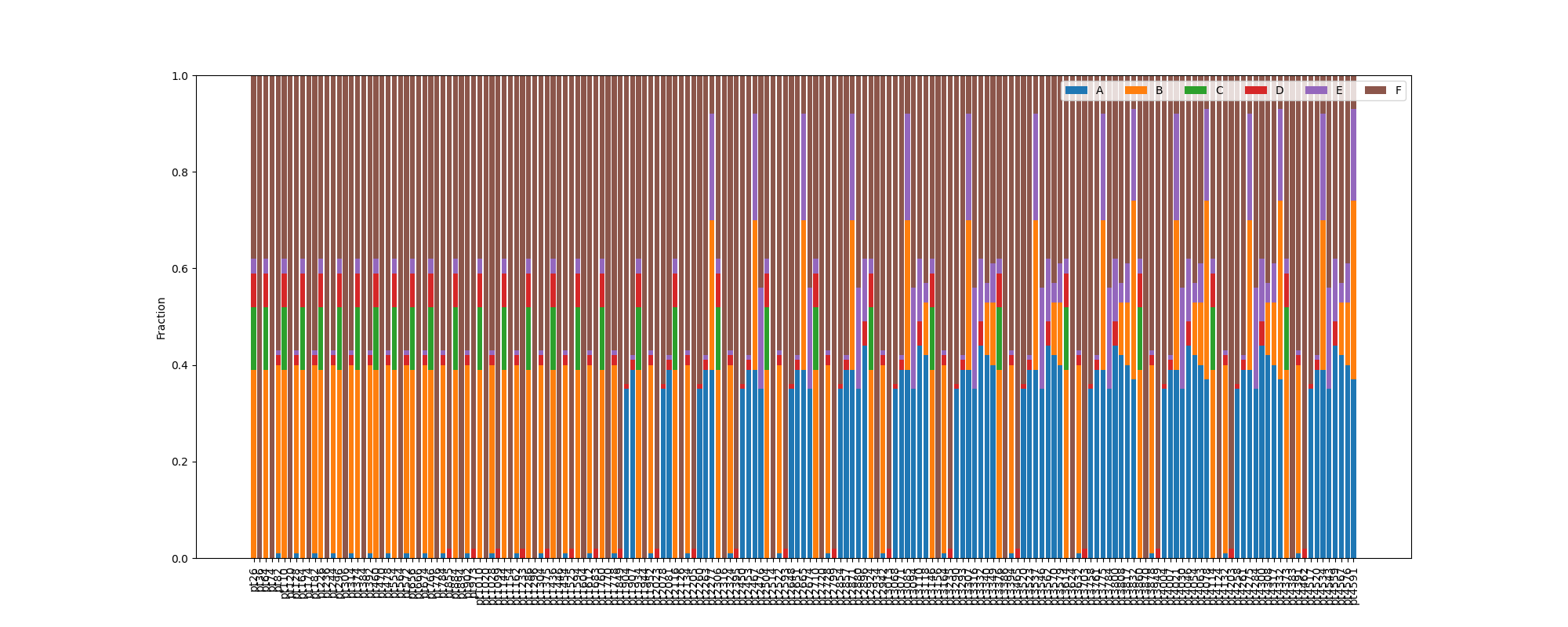
Designing high-performance materials typically requires testing thousands of formulations—a slow, expensive process. With 6 base photopolymers (A-F), there are infinite possible mixtures, making exhaustive testing impossible.
The goal was to demonstrate how Bayesian Optimization can accelerate material discovery by intelligently deciding which experiments to run next, maximizing properties like toughness, compression modulus, and strength simultaneously.
My Contribution
I implemented a probabilistic optimization loop:
- Probabilistic Modeling: Used Gaussian Processes (GP) to model the unknown relationship between chemical composition and material properties.
- Acquisition Strategy: Implemented Thompson Sampling to balance exploration (testing uncertain inputs) and exploitation (refining known good inputs).
- Multi-Objective Support: Optimized for multiple conflicting objectives to identify the Pareto Frontier of material performance.
Technical Approach
1. Gaussian Process Regression
Instead of a single prediction, a Gaussian Process predicts a probability distribution for every point in the design space. This gives us both a mean prediction and an uncertainty estimate (variance), which is crucial for safe exploration.
2. Exploration vs. Exploitation
Using Thompson Sampling, the algorithm samples a function from the GP posterior and selects the maximum. This naturally encourages exploring regions with high uncertainty (high variance) that could be optimal, while still exploiting regions known to be good.
Validation / Results
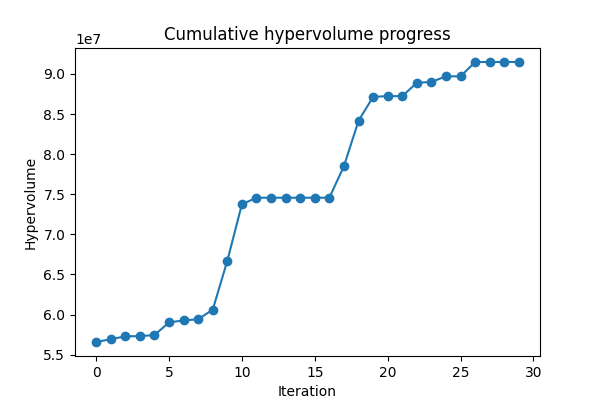
After just 30 iterations of optimization:
- 12 Pareto-optimal materials were discovered.
- 288× larger performance space explored compared to random sampling.
- Identified formulations with superior combinations of toughness and strength that were missed by intuition.

Broader Impact
This approach isn't limited to photopolymers. The same Bayesian Optimization framework can be applied to:
- Concrete formulations for 3D-printed buildings
- Alloy compositions for aerospace applications
- Pharmaceutical compounds for drug discovery